An alternative to one-hot encoding
(This is only semi-frivolous.)
When you have categorical data, and you want to encode it numerically for a numerical algorithm, there is no justification for using integers. That would be saying that e.g. category 0 is closer to category 1 than to category 4. It’s ok with a binary variable, even if conceptually it is categorical, because 0 and 1 (or -1 and 1 if you prefer) are equidistant from each other. But with three points, there are no 3 real numbers which are all equidistant from each other.
The standard solution is one-hot encoding (also known as “1-of-k” encoding): a vector of length n, with zeros in all places but one (and a one in that). The location indicates the category. Think of this as a projection into n-dimensional space. All the points are now 1 unit from the origin along the positive axes, and all are equidistant, in that space.
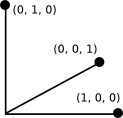
Example: suppose the categories are red, green and blue. We encode using three binary variables like this:
v1 v2 v3
Red 1 0 0
Green 0 1 0
Blue 0 0 1
Aside: one-hot encoding leads to sparse variables.
But you don’t need n dimensions: you only need n-1! If you have two categories, you can use real numbers -1 and 1. That is one dimension. If you have three categories, you can represent them equidistantly using two numbers. Think of them as the complex cube roots of 1. Complex numbers live in a two-dimensional plane:
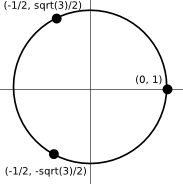
Using the same example again, see how we now only need two variables:
v1 v2
Red 1 0
Green -1/2 sqrt(3)/2
Blue -1/2 -sqrt(3)/2
If you have four categories, think of four points equidistant on a (3D) sphere, and so on. In general, let’s call this the spherical encoding of categories. If you have n categories, then they are represented as n equidistant points on the surface of a hypersphere of dimension n-1.
Advantage: compared to the one-hot encoding, you have one fewer variable! The curse of dimensionality becomes a less offensive swearword, like “feck” for example, instead of that other one (you know the one I mean).
Disadvantage: your model will be a lot harder to explain to your manager/customer/supervisor!
Empirical questions to be investigated: which algorithms perform differently with this encoding? Should you normalise all the variables independently?
Question regarding previous work to be investigated: has anyone tried this?